３次関数のグラフ
【高校数学の目次】
《数学Ⅰ・Ａ》
• 数と式　 • 根号計算 　• 場合の数.順列.組合せ 　• 確率　 • ２次関数　• ２次不等式　 • 集合・命題・条件・証明 　• 正弦定理,余弦定理
《数学Ⅱ・Ｂ》
• 指数関数.対数関数　 • 微分・積分　
《高校数学Ⅱ / 微分･積分の目次》　　　 が現在地
• 平均変化率　 • 極限値，不定形の極限　 • 導関数の定義 　 • 接線の方程式　 • 導関数の符号の求め方　 • 3次関数のグラフ（微分以前） 　 • (問題)平均変化率，関数の極限，極限値から定数を求める問題 　 • (問題)微分係数，導関数の定義　 • (問題)導関数の公式　 • (問題)増減と極値　 • (問題)最大最小,グラフと係数の符号,実数解の個数　 • センター試験.数Ⅱ微積(2013～)　 • 不定積分（数学II.多項式）　 • 不定積分2（展開）　 • 変数 t, y, r　 • 積分定数の決定　 • 定積分　 • 定積分の基本計算　 • 面積の求め方　 • 定積分と面積(1) 　 • 発展学習:定積分と面積(2) 　 • 曲線で囲まれた図形の面積　 • 絶対値付きの定積分(1)　 • 絶対値付きの定積分(2)（数学Ⅱ，入試問題）　 • 立体の体積　 • 定積分で定義される関数　
※この教材は，高校数学の基本問題の中の３次関数のグラフのページを作り直したものです．

■３次関数のグラフ･･･微分するまでに分かること
■３次関数のグラフの見方（その１）
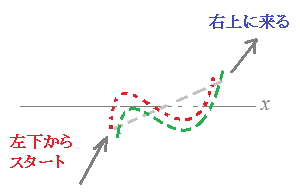
　３次関数のグラフ全体の増減の傾向を見るときは，x3の係数を見るとよい．
○　右の--図１--は
.y=1x3+2x2−3x+4
のグラフです．
　このグラフは，全体の傾向として
.「左下から右上へ向かって」
います．
　その理由は次のように考えることができます．
　例えば，x=10のとき，
x3=1000
2x2=200
−3x=−30
4
となって，大きさのほとんどはx3で決まり，他は小銭のようなものです．
　逆に，x=−10のとき，
x3=−1000
2x2=200
−3x=30
4
も，大きさのほとんどはx3で決まり，他は小銭のようなものです．

○　右の--図２--は
.y=2x3+5x−7
のグラフで，このグラフでもx=10のような大きな値では，大きさのほとんどは2x3で決まり，5x−7の値はわずかなものです．
○　　右の--図３--は
.y=−1x3+3x
のグラフです．
　このグラフは，全体の傾向として
.「左上から右下へ向かって」
います．
　その理由は次のように考えることができます．
　例えば，x=10のとき，
x3=1000
3x=30
となって，大きさのほとんどはx3で決まり，他は小銭のようなものです．
　逆に，x=−10のとき，
−1x3=1000
3x=−30
も，大きさのほとんどはx3で決まり，他は小銭のようなものです．

○　右の--図４--は
.y=−2x3+3x2
のグラフで，このグラフでもx=10のような大きな値では，大きさのほとんどは−2x3で決まり，3x2の値はわずかなものです．

【その１･･･要点】
　x3の係数が正　⇒　大きな傾向としては「左下から右上へ」
　x3の係数が負　⇒　大きな傾向としては「左上から右下へ」



■３次関数のグラフの見方（その２）
　３次関数のグラフ
.y=ax3+bx2+cx+d (a≠0)
とx軸すなわちy=0の直線との共有点（交点と接点）を調べるには，３次方程式
.ax3+bx2+cx+d=0
を解けばよい．

　特に，３次式ax3+bx2+cx+d=0 (a≠0)が
.a(x−α)(x−β)(x−γ)=0
の形に因数分解できるときは，３次方程式の解はx=α, β, γとなるから，これらが共有点のx座標になる．
○右の--図５--はy=(x+1)x(x−2)のグラフです．
　◆まず第１に，y=(x+1)x(x−2)=x3−x2−2xで，x3の係数が正だから，グラフは「左下から右上に」向かいます．
　◆x軸と交わる場所は，３次方程式を解いて求めます．
(x+1)x(x−2)=0から
x+1=0 → x=−1
x=0
x−2=0 → x=2
　◆以上の２つのことを考えて，「左下から入る」→「x=−1で交わる」→「x=0で交わる」→「x=2で交わる」→「右上に向かう」
　すると，--図５--のようなグラフが描けます．






○上の--図６--はy=−(x+2)(x+1)(x−1)のグラフです．
　◆まず第１に，y=−(x+2)(x+1)(x−1)=−1x3...で，x3の係数が負だから，グラフは「左上から右下に」向かいます．
　◆x軸と交わる場所は，３次方程式を解いて求めます．
−(x+2)(x+1)(x−1)=0から
x+2=0 → x=−2
x+1=0 → x=−1
x−1=0 → x=1
　◆以上の２つのことを考えて，「左上から入る」→「x=−2で交わる」→「x=−1で交わる」→「x=1で交わる」→「右下に向かう」
　すると，--図６--のようなグラフが描けます．

■重解（二重解，三重解）があるときのグラフの特徴

Ａ：y=a(x−α)(x−β)(x−γ)において，
α<β<γが互いに異なる値のとき，グラフは右の解説図Ａのようになります．
　上で述べた--図５--はα=−1, β=0, γ=2の場合になっています．
　--図６--はα=−2, β=−1, γ=1です．

Ｂ：小さい方の２つの解α, βがカレイの目玉のようにだんだん寄ってきて，とうとう重なってしまった場合（β=α）を考えると，
y=a(x−α)(x−α)(x−γ)=a(x−α)2(x−γ)のグラフはＢのようになります．
　例えば，α=−1, β=−1, γ=2の場合，方程式はy=a(x+1)2(x−2)となり，上のＢの図になります．
　x3の係数aが負の値の場合，例えばy=−2(x+1)2(x−2)のときは，下のＢの図になります．
■** これらの場合，グラフはx=α(=β)の所で「接点」となります．⇒横切らずに，元の側に戻ります．**■

Ｃ：大きい方の２つの解β, γが重なった場合（γ=β）は，
y=a(x−α)(x−β)(x−β)=a(x−α)(x−β)2のグラフはＣのようになります．
　例えば，α=−1, β=2, γ=2の場合，方程式はy=a(x+1)(x−2)2となり，上のＣの図になります．
　x3の係数aが負の値の場合，例えばy=−2(x+1)(x−2)2のときは，下のＣの図になります．
■** これらの場合も，グラフはx=β(=γ)の所で「接点」となります．⇒横切らずに，元の側に戻ります．**■

Ｄ：３つとも重なった場合（α=γ=β）は，
y=a(x−α)(x−α)(x−α)=a(x−α)3のグラフはＤのようになります．
　例えば，α=2, β=2, γ=2の場合，方程式はy=a(x−2)3となり，上のＤの図になります．
　x3の係数aが負の値の場合，例えばy=−(x−2)3のときは，下のＤの図になります．
■** これらの場合も，グラフはx=α(=β=γ)の所で「接点」となり，しかもその後向こう側に出ます．**■
--解説図--
※三重解を持つＤの図は，「単にx軸と交わっているのとは違います．」
　駅のホームで線路をよく見ると，ホームが３つあるような場合には，線路が単に交差しているのではなくて，直進もできさらに向こうの線路にも行けるように三重解の形に作ってあることが分かります．
【解，二重解，三重解でx軸に触った後の向き】…世間的・通俗的な解説～♪
○右の--図７--はy=(x+2)2(x−1)のグラフです．
　◆まず第１に，y=(x+2)2(x−1)=1x3...で，x3の係数が正だから，グラフは「左下から右上に」向かいます．
　◆x軸と交わる場所は，３次方程式を解いて求めます．
(x+2)2(x−1)=0から
x+2=0 → x=−2（二重解）
x−1=0 → x=1
　◆以上の２つのことを考えて，「左下から入る」→「x=−2で接するだけで元に戻る」→「x=1で交わる」→「右上に向かう」
　すると，--図７--のようなグラフが描けます．
○右の--図８--はy=(x+2)(x−1)2のグラフです．
　◆まず第１に，y=(x+2)(x−1)2=1x3...で，x3の係数が正だから，グラフは「左下から右上に」向かいます．
　◆x軸と交わる場所は，３次方程式を解いて求めます．
(x+2)(x−1)2=0から
x+2=0 → x=−2
x−1=0 → x=1（二重解）
　◆以上の２つのことを考えて，「左下から入る」→「x=−2で交わる」→「x=1で接するだけで元に戻る」→「右上に向かう」
　すると，--図８--のようなグラフが描けます．
○右の--図９--はy=−(x+1)2(x−2)のグラフです．
　◆まず第１に，y=−(x+1)2(x−2)=−1x3...で，x3の係数が負だから，グラフは「左上から右下に」向かいます．
　◆x軸と交わる場所は，３次方程式を解いて求めます．
(x+1)2(x−2)=0から
x+1=0 → x=−1（二重解）
x−2=0 → x=2
　◆以上の２つのことを考えて，「左上から入る」→「x=−1で接するだけで元に戻る」→「x=2で交わる」→「右下に向かう」
　すると，--図９--のようなグラフが描けます．


○上の--図10--はy=(x−1)3のグラフです．
　◆まず第１に，y=(x−1)3=1x3...で，x3の係数が正だから，グラフは「左下から右上に」向かいます．
　◆x軸と交わる場所は，３次方程式を解いて求めます．
(x−1)3=0から
x−1=0 → x=1（三重解）
　◆以上の２つのことを考えて，「左下から入る」→「x=1で接するが反対側に出る」→「右上に向かう」
　すると，--図10--のようなグラフが描けます．

■実数解が１つだけあるときのグラフの特徴

Ｅ：
y=a(x−α)(x2+1)
y=a(x−α)(x2+x+1)
のように，３次方程式が実数解を１つだけ持っていて，残り２つは虚数解という場合
右図11や12のようにx軸との交点が１つだけあります．
○右の--図11--はy=(x−1)(x2+1)のグラフです．
　◆まず第１に，y=(x−1)(x2+1)=1x3...で，x3の係数が正だから，グラフは「左下から右上に」向かいます．
　◆x軸と交わる場所は，３次方程式を解いて求めます．
(x−1)(x2+1)=0から
x−1=0 → x=1
x2+1=0 → 判別式が負だから虚数解（実数解なし）
　◆以上の２つのことを考えて，「左下から入る」→「x=1で交わる→「右上に向かう」
　すると，--図11--のようなグラフが描けます．
それじゃ～
y=x−1の直線と同じじゃないかよ．

y=x−1と違って，
y=(x2+1)(x−1)になっているので，傾きが変化するのです．
どこで曲がるか，わからん．

おっしゃる通りで，曲がり方は「微分」を使わないと言えません．
　この頁では微分を使わない範囲までしか扱っていないので，深入りは避けます．
○右の--図12--はy=(x−2)(x2+2x+3)のグラフです．
　◆まず第１に，y=(x−2)(x2+2x+3)=1x3...で，x3の係数が正だから，グラフは「左下から右上に」向かいます．
　◆x軸と交わる場所は，３次方程式を解いて求めます．
(x−2)(x2+2x+3)=0から
x−2=0 → x=2
x2+2x+3=(x+1)2+2=0 → 判別式が負だから虚数解（実数解なし）
　◆以上の２つのことを考えて，「左下から入る」→「x=2で交わる→「右上に向かう」
　すると，--図12--のようなグラフが描けます．
x=2で交わるのは分かるが，曲がり方が分からん

x=0のときにy=−6になるので，あとは滑らかに結びます．

（難しい読み物）
※　ここまで，３次方程式の解について調べてきましたが
ｎ次方程式は，複素数の範囲で（重解はその重複度だけ数えるものとして）ｎ個の解を持ちます．［代数学の基本定理］
したがって，３次方程式は複素数の範囲で３個の解を持ちます．
　次に，この頁で扱っている，実係数の３次関数y=ax3+bx2+cx+d (a≠0)について考えると
実軸x, y平面上のグラフを考えるときに，虚数係数の３次関数は考えない．虚数係数だとグラフは描けないから．
　３次方程式ax3+bx2+cx+d=0 (a≠0)の実数解の個数（重解はその重複度だけ数えるものとする）は，
■ア　実数解０個（実数解なし）と虚数解３個：←このようなことは起らない．
○イ　実数解１個と虚数解２個
■ウ　実数解２個と虚数解１個：←このようなことは起らない．
○エ　実数解３個と虚数解０個（虚数解なし）
　エを細かく分けたものが上述のＡ，Ｂ，Ｃ，Ｄとなっている．

　残りのア，イ，ウを考えるには，次の定理が鍵になる．
「実係数のｎ次方程式が虚数解p+qi (q≠0)を持てば，その共役複素数p−qiもまた解となる．」
(1) これにより，実係数の１次方程式ax+b=0（a,bは実数）は虚数解を持たないことが間接的に分かる．なぜなら，もし虚数x=p+qi (q≠0)が解ならば，その共役複素数もx=p−qi (q≠0)も解となり，解が２個あることになり，代数学の基本定理と矛盾するから．
　もちろん，直接的にx=−は実数と言うこともできる．
(2) 実係数の２次方程式ax2+bx+c=0（a≠0,b,cは実数）は，実数解を２つ持つ場合（重解となる場合も含む）と虚数解を２つ持つ場合しかないことが分かる．なぜなら，もし，実数解１つ（x=α）と虚数解１つβ=p+qi (q≠0)を持てば，β=p−qiも解となり，２次方程式に解が３個あることになって，代数学の基本定理と矛盾するから．
実数解が２つある例：(x+2)(x−1)=0 → x=−2, 1
虚数解が２つある例：x2+x+1=0 → x=
(3) 実係数の３次方程式ax3+bx2+cx+d=0（a≠0,b,c,dは実数）の解を調べると，ここまでの内容と同様に虚数解は０個か２個しかあり得ないから，上の分類のイとエのみが可能で，アとウは不可能となる．
実係数の３次方程式ax3+bx2+cx+d=0（a>0,b,c,dは実数）の実数解が「ない」ということは起りえなくて，「少なくとも１つはある」ということは，右のような図によっても分かる．
　左下からスタートして，右上に行くのであるから，少なくとも１回はx軸に触れる．もちろん，赤で示したように３回触れる場合（異なる３個の実数解がある場合）や，緑で示したように２回触れる場合（実数の重解１つと他の１つの実数解）もある．

（参考）
　次の問題では，数式を GoogleChart APIで表し，グラフを Google Chart Toolsで描き，採点をjavascriptで行っています．
　ご利用のネットワーク環境によっては，グラフの描画に少し時間がかかる場合があります．
【問題】　次の３次関数の形を答えてください．
はじめに左の欄から３次関数を選び，
続いて右のグラフを選んでください．
やり直すときは，右のグラフを次々に選ぶのでなく，左の３次関数を選び直すことから始めてください．
HELPのメッセージは，下の 　に出ます．







コメント

コメントを投稿