|
• 数と式 • 根号計算 • 場合の数.順列.組合せ • 確率 • 2次関数 • 2次不等式 • 集合・命題・条件・証明 • 正弦定理,余弦定理 《数学Ⅱ・B》 • 指数関数.対数関数 • 微分・積分 ♪♥ この教材は,高校数学の基本問題のうち,面積の求め方の「マイナーチェンジありカバー版」「広告なし」「パソコン用」ページです. ♫♣ 元の教材が通信トラブルなどで読めないときに,こちらを使ってください.なお,学習の記録は付いていません. |
|
■面積 解説 (ア) y=f(x)のグラフがx軸よりも上にあるとき (f(x)≧0のとき)定積分は面積を表わします。 |
(イ) y=f(x)のグラフがx軸よりも下にあるとき (f(x)≦0のとき)y=-f(x)のグラフを作ると,このグラフはx軸よりも上にあるので,符号を変えた定積分は面積を表わします。 |
|
(ウ) f(x)≧g(x)≧0のとき,次のように2つの面積の差が2曲線の間にある図形の面積になります。(切り紙のイメージで考えます。) |
(エ) f(x)≧g(x)であれば,形・面積が変わらないように持ち上げるとg(x)≧0となり2つの面積の差が2曲線の間にある図形の面積になります。→(ウ)になります。 |
| ◆◆まとめ◆◆・・・以上の(ア)~(エ)は(エ)でまとめることができます。 | ||
| ○ 面積は ∫{ (上) - (下) }dx ・・・ x軸より下にあってもこれでよい。 | ||
| 「キュウリもみ」を作ったことがありますか? 「(上)-(下)という長さ」のキュウリの断片を x軸上に集めているのと同じことです。 |
||
| 初めの公式の見直し:(ア) 上がy=f(x),下がy=0と見ます。 |
初めの公式の見直し:(イ) 上がy=0,下がy=f(x)と見ます。 |
|
|
■例題 (1) y=x2,x軸,x=1,x=2の直線で囲まれる図形の面積   |
(2) y=x2-xの曲線とx軸とで囲まれる図形の面積  |
| (3) y=-x2+4x と y=x とで囲まれる図形の面積 |
(4) y=4(x3-x) と x軸とで囲まれる図形の面積 ※上下が変わるときは,区間を分けて計算します。 |
|
【問題1】 次の図形の面積を求めてください.
(1)
解答を見るy=x2,x軸,x=0, x=3の直線で囲まれる図形の面積 |
(2)
解答を見るy=x3−9x,x軸で囲まれる図形の面積 |
|
(3)
解答を見るy=x2のグラフとy=9の直線で囲まれる図形の面積
右図のように,区間−3<<3において,関数y=x2のグラフはy=9の直線よりも下にあるから
※この問題のように,「2曲線y=x2とy=9の交点間の面積」となっている図では,発展学習に出るいわゆる「6分の1公式も使える」
において, |
(4)
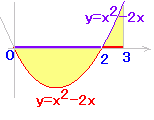
解答を見るy=x2−2x,x軸,x=3の直線で囲まれる図形の面積
右図のように,区間0<x<2において,関数y=x2−2xのグラフはx軸よりも下にあり,区間2<x<3において,関数y=x2−2xのグラフはx軸よりも上にあるから
※この問題のように,「2曲線の交点間」となっていない図では,いわゆる「6分の1公式は使えない」ので注意 |
|
(5)
解答を見るy=x2−2x+3のグラフとy=x+3の直線で囲まれる図形の面積  右図のように,区間0<<3において,関数y=x2−2x+3のグラフはy=x+3の直線よりも下にあるから
右図のように,区間0<<3において,関数y=x2−2x+3のグラフはy=x+3の直線よりも下にあるから
※この問題のように,「2曲線y=x2−2x+3とy=x+3の交点間の面積」となっている図では,発展学習に出るいわゆる「6分の1公式も使える」
において, |
(6)
解答を見るkを定数とするとき,y=x2のグラフと 直線y=2kx−(k2+k)の直線で囲まれる図形の面積
桃色の縦棒のどこかをクリックすると,対応するグラフが表示されます
kの現在値
の解は 上図のように,区間k<x<k+1において,関数y=x2のグラフは直線y=(2k+1)x−k(k+1)よりも下にあるから ※kの値に依らずに一定値をとる |










 右図のように,区間
右図のように,区間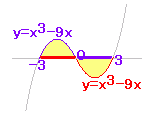 右図のように,区間
右図のように,区間
コメント