数学Ⅱ・微分積分

【高校数学の目次】 《数学Ⅰ・Ａ》 • 数と式　 • 根号計算 　• 場合の数.順列.組合せ 　• 確率　 • ２次関数　• ２次不等式　 • 集合・命題・条件・証明 　• 正弦定理,余弦定理 《数学Ⅱ・Ｂ》 • 指数関数.対数関数　 • 微分・積分　 《高校数学Ⅱ / 微分･積分の目次》　　　 が現在地 • 平均変化率　 • 極限値，不定形の極限　 • 導関数の定義 　 • 接線の方程式　 • 導関数の符号の求め方　 • 3次関数のグラフ（微分以前） 　 • (問題)平均変化率，関数の極限，極限値から定数を求める問題 　 • (問題)微分係数，導関数の定義　 • (問題)導関数の公式　 • (問題)増減と極値　 • (問題)最大最小,グラフと係数の符号,実数解の個数　 • センター試験.数Ⅱ微積(2013～)　 • 不定積分（数学II.多項式）　 • 不定積分2（展開）　 • 変数 t, y, r　 • 積分定数の決定　 • 定積分　 • 定積分の基本計算　 • 面積の求め方　 • 定積分と面積(1) 　 • 発展学習:定積分と面積(2) 　 • 曲線で囲まれた図形の面積　 • 絶対値付きの定積分(1)　 • 絶対値付きの定積分(2)（数学Ⅱ，入試問題）　 • 立体の体積　 • 定積分で定義される関数　 ♪♥ この教材は，高校数学の基本問題のうち，センター試験.数Ⅱ微積(2013～)のマイナーチェンジありのカバー版です． ♫♣ 元の教材が通信トラブルなどで読めないときに，こちらを使ってください．なお，学習の記録は付いていません．

== センター試験.数Ⅱ微積(2013～) == 【2013年度センター試験.数学Ⅱ･B】第2問（必答問題） 　aを正の実数として，xの関数f(x)を f(x)=x3−3a2x+a3 とする。 　関数y=f(x)は，x=アイで極大値ウaエをとり，x=オで極小値カaキをとる。このとき，2点 アイ，ウaエ，オ，カaキ と原点を通る放物線 y=クx2−ケaコx をCとする。原点におけるCの接線ℓの方程式は y=サシaスx である。また，原点を通りℓに垂直な直線mの方程式は y= 1 セaソ x である。

解説を読む f’(x)=3x2−3a2=3(x+a)(x−a) a>0だから，増減表は次のようになる． x ··· −a ··· a ··· f'(x) + 0 − 0 + f(x) 3a3 −a3 x=−aのとき，極大値3a3をとる→アイ,ウ,エ x=aのとき，極小値−a3をとる→オ,カ,キ 3点O(0, 0), P(−a, 3a3), Q(a, −a3)を通る放物線の方程式を y=Ax2+Bx+C とおく． O(0, 0)を通るから C=0･･･(#1) P(−a, 3a3)を通るから 3a3=Aa2−Ba+C･･･(#2) Q(a, −a3)を通るから −a3=Aa2+Ba+C･･･(#3) (#1)(#2)(#3)より A=a, B=−2a2, C=0 y=ax2−2a2x→ク,ケ,コ ⇒(#4)放物線C (#4)を微分すると y'=2ax−2a2 x=0のとき，y'=−2a2だから，接線ℓの方程式は y=−2a2x→サシ,ス 垂線mの方程式は →セ,ソ ♪∀～勝手に批評～個人の感想～∅♥ 　ここまでは，誰でもできる．受験生間の差は出ない． →解説を隠す←

x軸に関して放物線Cと対称な放物線 y=−クx2+ケaコx をDとする。Dとℓで囲まれた図形の面積Sは S= タチ ツ aテ である。 放物線Cと直線mの交点のx座標は，0と 4aト+1 2aナ である。Cとmで囲まれた図形の面積をTとする。 S=Tとなるのはaテ= ニ ヌ のときであり，このと き，S= ネ ノ である。

解説を読む 放物線C(#4)をx軸に関して対称に移動すると y=−ax2+2a2x⇒放物線D 放物線Dと接線ℓ y=−2a2x の交点は −ax2+2a2x=−2a2x ax2−4a2x=0 ax(x−4a)=0 x=0, 4a この計算は，いわゆる「6分の1公式」を使って短縮的に書いてもよい →タチ,ツ,テ 放物線Cと直線mの交点は y=ax2−2a2x･･･放物線C ･･･直線m 代入してyを消去する x=0または→ト,ナ ←いわゆる「6分の1公式」 S=Tとおくと →ニ,ヌ →ネ,ノ ♪∀～勝手に批評～個人の感想～∅♥ 　内容的に高度なものではないが,方程式C, D,直線ℓ，mなどが，ずいぶん離れた場所に書かれていて，元の場所を探すだけで時間が取られる． 　anの変形が満載されているが，これがセンター試験としての指数計算の出題の仕方だと思えばよい．（公式暗記程度の問題から垢抜けした良問） →解説を隠す←

【2014年度センター試験.数学Ⅱ･B】第2問（必答問題） 　pを実数とし，f(x)=x3−pxとする。 (1)　関数f(x)が極値をもつためのpの条件を求めよう。f(x)の導関数は，f'(x)=アxイ−pである。したがって，f(x)がx=aで極値をとるならば， 　アxイ−p=ウが成り立つ。さらに，x=aの前後でのf'(x)の符号の変化を考えることにより，pが条件エを満たす場合は，f(x)は必ず極値をもつことがわかる。エに当てはまるものを，次の⓪～④のうちから一つ選べ。 　⓪ p=0　① p>0　② p≧0　③ p<0　④ p≦0

解説を読む (1) f'(x)=3x2−p→ア,イ x=aで極値をとるならば，3a2−p=0→ウ pが条件p>0:①を満たす場合は，f(x)は極値をもつ→エ →解説を隠す←

(2)　関数f(x)がで極値をとるとする。また，曲線y=f(x)をCとし，C上の点をAとする。 　f(x)がで極値をとることから，p=オであり，f(x)はx=カキで極大値をとり，x=クで極小値をとる。

解説を読む (2) 3a2−p=0 (p>0) のとき極値をとるから p>0により p=3→オ p=3のときだから 増減表は次のようになる． x ··· −1 ··· 1 ··· f'(x) + 0 − 0 + f(x) 2 −2 x=−1で極大値をとり，x=1で極小値をとる→カキ,ク →解説を隠す←

曲線Cの接線で，点Aを通り傾きが0でないものをℓとする。ℓの方程式を求めよう。ℓとCの接点のx座標をbとすると，ℓは点(b, f(b))におけるCの接線であるから，ℓの方程式はbを用いて y=ケb2−コ(x−b)+f(b) と表すことができる。また，ℓは点Aを通るから，方程式 サb3−シb2+1=0 を得る。この方程式を解くと，b=ス， セソ タ であ るが，ℓの傾きが0でないことから，ℓの方程式は y= チツ テ x+ ト ナ である。

解説を読む y=(3b2−3)(x−b)+f(b)→ケ,コ が点A(1, −2)を通るから −2=(3b2−3)(1−b)+(b3−3b) 2b3−3b2+1=0→サ,シ (b−1)(2b2−b−1)=0 (b−1)2(2b+1)=0 →ス,セソ b≠0だから このとき，直線ℓの方程式は →チツ,テ,ト,ナ →解説を隠す←

点Aを頂点とし，原点を通る放物線をDとする。ℓとDで囲まれた図形のうち，不等式x≧0の表す領域に含まれる部分の面積Sを求めよう。Dの方程式は y=ニx2−ヌx であるから，定積分を計算することにより，S= ネノ 24 となる。

解説を読む Dの方程式は y=2(x−1)2−2=2x2−4x→ニ,ヌ →ネノ →解説を隠す←

【2015年度センター試験.数学Ⅱ･B】第2問（必答問題） (1)　関数のx=aにおける微分係数f'(a)を求めよう。hが0でないとき，xがaからa+hまで変化す るときのf(x)の平均変化率はア+ h イ である。 したがって，求める微分係数は f'(a)= lim h→ウ ア+ h イ =エ である。

解説を読む (1) xがaからa+hまで変化するときのf(x)の平均変化率は →ア,イ 微分係数は →ウ,エ →解説を隠す←

(2)　放物線をCとし，C上に点をとる。ただし，a>0とする。点PにおけるCの接線ℓの方程式は y=オx− 1 カ a2 である。直線ℓとx軸との交点Qの座標は キ ク ，0 である。点Qを通りℓに垂直な直線をmとすると,mの方程式は y= ケコ サ x+ シ ス である。

解説を読む (2) f'(a)=aだから，接線ℓの方程式は →オ,カ y=0とおくと →キ,ク ℓに垂直な直線mの傾きは を通り，傾きの直線の方程式は →ケコ,サ,シ,ス →解説を隠す←

直線mとy軸との交点をAとする。三角形APQの面積をSとおくと S= a(a2+セ) ソ となる。また，y軸と線分APおよび曲線Cによって囲まれた図形の面積をTとおくと T= a(a2+タ) チツ となる。

解説を読む において，AQとQPは垂直だから →セ,ソ 直線APの方程式は 曲線Cの方程式は 積分区間は0≦x≦aだから，求める面積は →タ,チツ ♪∀～勝手に批評～個人の感想～∅♥ 　6分の1公式ではできない，基本に忠実な良問だと思う →解説を隠す←

a>0の範囲におけるS−Tの値について調べよう。 S−T= a(a2−テ) トナ である。a>0であるから，S−T>0となるようなaのとり得る値の範囲はa>ニ　である。また，a>0のときのS−Tの増減を調べると，S−Tはa=ヌで最小値 ネノ ハヒ をとることがわかる。

解説を読む →テ,トナ a>0のときS−T>0となるaの範囲を求めると →ニ a>0のときのS−Tの増減は次の表のようになる a 0 ··· 1 ··· (S−T)' × − 0 + S−T × a=1のとき，最小値をとる→ヌ,ネノ,ハヒ →解説を隠す←

【2016年度センター試験.数学Ⅱ･B】第2問（必答問題） 　座標平面上で，放物線をC1とし，放物線 をC2とする。 (1)　実数aに対して，2直線x=a, x=a+1とC1，C2で囲まれた図形Dの面積Sは 1 ア x2+ 1 イ = a2 ウ + a エ + オ カキ である。Sはa= クケ コ で最小値 サシ スセ をとる。

解説を読む (1) x≧0のとき，だから →ア,イ →ウ,エ,オ,カキ a − 0 + S のとき，最小値をとる→クケ,コ,サシ,スセ →解説を隠す←

(2)　4点(a, 0), (a+1, 0), (a+1, 1), (a, 1)を頂点とする正方形をRで表す。aがa≧0の範囲を動くとき，正方形Rと(1)の図形Dの共通部分の面積をTとおく。Tが最大となるaの値を求めよう。 　直線y=1は，C1と(±ソ, 1)で,C2と(±タ, 1)で交わる。したがって，正方形Rと図形Dの共通部分が空集合にならないのは，0≦a≦チのときである。

解説を読む --図1-- 　を解くと，x=±1 C1との交点は(±1, 1)→ソ 　を解くと，x=±2 C2との交点は(±2, 1)→タ 　右図の赤枠で示した正方形Rが図形Dとの共通部分がある限界だから，0≦a≦2→チ →解説を隠す←

ソ≦a≦チのとき，正方形Rは放物線C1とx軸の間にあり，この範囲でaが増加するとき,Tはツ。ツに当てはまるものを，次の⓪～②のうちから一つ選べ。 ⓪　増加する　　①　減少する　　②　変化しない 　したがって，Tが最大になるaの値は，0≦a≦ソの範囲にある。 　0≦a≦ソのとき，(1)の図形Dのうち，正方形Rの外側にある部分の面積Uは U= a3 テ + a2 ト である。よって，0≦a≦ソにおいて T=− a3 ナ − a2 ニ + a ヌ + オ カキ ･･･① である。①の右辺の増減を調べることにより，Tは a= ネノ+ハ　 ヒ で最大値をとることがわかる。

解説を読む 　図1から分かるように，1≦a≦2のとき，aが増加すれば，R, Dの共通部分Tの面積は減少する①→ツ 　図1において，DのうちでRの外側にある部分Uの面積は →テ,ト →ナ,ニ,ヌ →ネノ,ハ,ヒ a 0 1 × + 0 − × T × 最小 × →解説を隠す←

【2017年度センター試験.数学Ⅱ･B】第2問（必答問題） 　Oを原点とする座標平面上の放物線y=x2+1をCとし，点(a, 2a)をPとする。 (1)　点Pを通り，放物線Cに接する直線の方程式を求めよう。 　C上の点(t, t2+1)における接線の方程式は y=アtx−t2+イ である。この直線がPを通るとすると，tは方程式 t2−ウat+エa−オ=0 を満たすから，t=カa−キ，クである。よって，a≠ケのとき，Pを通るCの接線は2本あり，それらの方程式は y=コa−サx−シa2+スa･･･① と y=セx である。

解説を読む (1) y'=2xだから，接線の方程式は y−(t2+1)=2t(x−t) y=2tx−t2+1→ア,イ この直線がP(a, 2a)を通るとき 2a=2ta−t2+1 t2−2ta+(2a−1)=0 {t−(2a−1)}(t−1)=0 t=2a−1, 1→カ,キ,ク 2a−1≠1のとき，すなわちa≠1のとき，接線は2本になる y=2(2a−1)x−(2a−1)2+1 =(4a−2)x−4a2+4a→コ,サ,シ,ス① および y=2x→セ →解説を隠す←

(2)　(1)の方程式①で表される直線をℓとする。ℓとy軸との交点をR(0, r)とすると，r=−シa2+スaである。r>0となるのは，ソ<a<タのときであり，このとき，三角形OPRの面積Sは S=チaツ−aテ となる。

解説を読む (2) 方程式①:y=(4a−2)x−4a2+4aがR(0, r)を通るから r=−4a2+4a r>0となるのは −4a2+4a>0 4a2−4a<0 4a(a−1)<0 0<a<1→ソ,タ OR=r(>0)，Pのx座標は(0<)a(<1)だから，△OPRの面積は →チ,ツ,テ ※注 ♪∀～勝手に批評～個人の感想～∅♥ ※注：とすると，チが2文字になるから，を解答とするようであるが，トンチ遊びのようで，筆者には良い感じがしない →解説を隠す←

ソ<a<タのとき，Sの増減を調べると，Sは a= ト ナ で最大値 ニ ヌネ をとることがわかる。 (3)　ソ<a<タのとき，放物線Cと(2)の直線ℓおよび2直線x=0, x=aで囲まれた図形の面積をTとすると T= ノ ハ a3−ヒa2+フ である。 ト ナ ≦a<タの範囲において,Tはヘ。 　ヘに当てはまるものを，次の⓪～⑤のうちから一つ選べ。 ⓪ 減少する　　① 極小値をとるが，極大値はとらない ② 増加する　　③ 極大値をとるが，極小値はとらない ④ 一定である　⑤ 極小値と極大値の両方をとる

解説を読む a 0 1 S' × + 0 − × S × × で最大値をとる→ト,ナ,ニ,ヌネ 放物線Cの方程式は y=x2+1 (2)の直線ℓの方程式は y=(4a−2)x−4a2+4a これらの差を区間0≦x≦aで積分する →ノ,ハ,ヒ,フ において増加， だからのとき a 1 T' 0 + T したがって，②増加する→ヘ →解説を隠す←

【2018年度センター試験.数学Ⅱ･B】第2問（必答問題） 〔1〕　p>0とする。座標平面上の放物線y=px2+qx+rをCとし，直線y=2x−1をℓとする。Cは点A(1, 1)においてℓと接しているとする。 (1)　qとrを，pを用いて表そう。放物線C上の点Aにおける接線ℓの傾きはアであることから， q=イウp+エがわかる。さらに，Cは点Aを通ることから，r=p−オとなる。

解説を読む [1](1) y=2x−1のとき，y'=2だから 　接線ℓの傾きは2→ア y=px2+qx+rについて，y'=2px+q 　点A(1, 1)における接線の傾きは，2p+q=2 　したがって，q=−2p+2→イウ,エ (#1) 放物線y=px2+qx+rが点A(1, 1)を通るから 　1=p+q+r (#2) (#2)に(#1)を代入 　1=p+(−2p+2)+r 　r=p−1→オ (#3) →解説を隠す←

(2)　>1とする。放物線Cと直線ℓおよび直線x=で囲まれた図形の面積Sは S= p カ キクケ である。また，x軸とℓおよび2直線x=1, x=で囲まれた図形の面積Tは，T=コ−である。 　U=S−Tはで極値をとるとする。このとき，p=サであり，の範囲でU=0となるの値をと すると，= シ+ス　 セ である。の範囲 でUはソ。　ソに当てはまるものを，次の⓪～④のうちから一つ選べ。 ⓪つねに増加する ①つねに減少する ②正の値のみをとる ③負の値のみをとる ④正と負のどちらの値もとる 　p=サのとき，におけるUの最小値はタチである。

解説を読む (2) →カ,キ,ク,ケ →コ のときとなる場合 p=3→サ このとき だから≒2.6→シ,ス,セ 1 2 U' × − 0 + × U 0 −1 0 の範囲でUは負の値のみとる→③ソ におけるUの最小値は−1→タチ →解説を隠す←

〔2〕　関数f(x)はx≧1の範囲でつねにf(x)≦0を満たすとする。t>1のとき，曲線y=f(x)とx軸および2直線x=1, x=tで囲まれた図形の面積をWとする。tがt>1の範囲を動くとき，Wは，底辺の長さが2t2−2，他の2辺の長さがそれぞれt2+1の二等辺三角形の面積とつねに等しいとする。このとき，x>1におけるf(x)を求めよう。 　F(x)をf(x)の不定積分とする。一般に，F'(x)=ツ，W=テが成り立つ。ツ，テに当てはまるものを，次の⓪～⑧のうちから一つずつ選べ。ただし，同じものを選んでもよい。 ⓪ −F(t) ① F(t) ② F(t)−F(1) ③ F(t)+F(1) ④ −F(t)+F(1) ⑤ −F(t)−F(1) ⑥ −f(x) ⑦ f(x) ⑧ f(x)−f(1) 　したがって，t>1において f(t)=トナtニ+ヌ である。よって，x>1におけるf(x)が分かる。

解説を読む 〔2〕 F'(x)=f(x)→⑦ ツ →④ テ 右図の直角三角形DEFにおいて，DF=t2+1，EF=t2−1だから，三平方の定理により DE2+EF2=DF2 DE2+(t2−1)2=(t2+1)2 DE2=4t2 DE=2t (t>1) W=2t(2t2−2)/2=2(t3−t)となるから f(t)=−W'(t)=−2(3t2−1)=−6t2+2→トナ,ニ,ヌ ♪∀～勝手に批評～個人の感想～∅♥ 　この問題の不定積分という用語と記号について，筆者の感想は別紙にあります →解説を隠す←

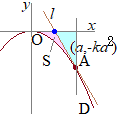
【2019年度センター試験.数学Ⅱ･B】第2問（必答問題） 　p, qを実数とし，関数f(x)=x3+px2+qxはx=−1で極値2をとるとする。また，座標平面上の曲線y=f(x)をC，放物線y=−kx2をD，放物線D上の点(a, −ka2)をAとする。ただし，k>0, a>0である。 (1)　関数f(x)がx=−1で極値をとるので，f'(−1)=アである。これとf(−1)=2より，p=イ，q=ウエである。よって，f(x)はx=オで極小値カキをとる。

解説を読む (1) f(x)=x3+px2+qxを微分すると f'(x)=3x2+2px+q したがって f'(−1)=3−2+q=0→ア　･･･(#1) また，題意により f(−1)=−1+p−q=2　･･･(#2) (#1)(#2)をp, qの連立方程式として解くと p=0, q=−3→イ,ウエ f(x)=x3−3x f'(x)=3x2−3=3(x+1)(x−1) として増減表を作る x ··· −1 ··· 1 ··· f'(x) + 0 − 0 + f(x) 2 −2 よって，f(x)はx=1で極小値−2をとる。 →解説を隠す←

(2)　点Aにおける放物線Dの接線をℓとする。Dとℓおよびx軸で囲まれた図形の面積Sをaとkを用いて表そう。 　ℓの方程式は y=クケkax+kaコ　･･･① と表せる。ℓとx軸の交点のx座標は サ シ であり，D とx軸および直線x=aで囲まれた図形の面積は k ス aセ である。よって，S= k ソタ aセである。

解説を読む D:y=−kx2について，y'=−2kx x=aのとき，y=−ka2, y'=−2kaだから，接線ℓの方程式は y+ka2=−2ka(x−a) y=−2kax+ka2→クケ,コ　(#3) (#3)においてy=0とおくと，ℓとx軸の交点の座標が求まる． →サ,シ Dとx軸および直線x=aで囲まれた図形の面積（右図の桃色で示した部分と水色で示した部分の和）は →ス,セ 右図の水色で示した部分の面積は だから →ソタ →解説を隠す←

(3)　さらに，点Aが曲線C上にあり，かつ(2)の接線ℓがCにも接するとする。このときの(2)のSの値を求めよう。 AがC上にあるので，k= チ ツ −テである。 　ℓとCの接点のx座標をbとすると，ℓの方程式はbを用いて y=ト(b2−ナ)x−ニb3　･･･② と表される。

解説を読む 点A(a, −ka2)が曲線Cy=x3−3x上にあるから −ka2=a3−3a a>0だからa2で割れる →チ,ツ,テ 点(b, b3−3b)における曲線Cの接線の方程式は y−(b3−3b)=(3b2−3)(x−b) y=3(b2−1)x−2b2→ト,ナ,ニ →解説を隠す←

②の右辺をg(x)とおくと f(x)−g(x)=(x−ヌ)2(x+ネb) と因数分解されるので，a=−ネbとなる。①と②の 表す直線の傾きを比較することにより,a2= ノハ ヒ である。 したがって，求めるSの値は フ ヘホ である。

解説を読む f(x)−g(x)=x3−3x−3(b2−1)x+2b3 =x3−3b2x+2b3 ここでx=bを代入すると0になるから，因数定理を用いて因数分解する f(x)−g(x)=(x−b)(x2+bx−2b2) =(x−b)2(x+2b)→ヌ,ネ ①は，y=−2kax+ka2 ②は，y=3(b2−1)x−2b2 これらの傾きを比較すると −2ka=3(b2−1) さらに も使うと →ノハ,ヒ →フ,ヘホ →解説を隠す←

【2020年度センター試験.数学Ⅱ･B】第2問（必答問題） 　a>0とし，f(x)=x2−(4a−2)x+4a2+1とおく。座標平面上で，放物線y=x2+2x+1をC，放物線y=f(x)をDとする。また，ℓをCとDの両方に接する直線とする。 (1)　ℓの方程式を求めよう。 　ℓとCは点(t, t2+2t+1)において接するとすると，ℓの方程式は y=(アt+イ)x−t2+ウ　･･･① である。また，ℓとDは点(s, f(s))において接するとすると，ℓの方程式は y=(エs−オa+カ)x −s2+キa2+ク　･･･② である。ここで，①と②は同じ直線を表しているので，t=ケ，s=コaが成り立つ。 　したがって，ℓの方程式はy=サx+シである。

解説を読む (1) Cについて，y=x2+2x+1を微分すると，y'=2x+2 したがって，(t, t2+2t+1)における接線の方程式は y−(t2+2t+1)=(2t+2)(x−t) y=(2t+2)x−t2+1→ア,イ,ウ　① また，Dについて，y=x2−(4a−2)x+4a2+1を微分すると，y'=2x−(4a−2) したがって，(s, f(s))=(s, s2−(4a−2)s+4a2+1)における接線の方程式は y−(s2−(4a−2)s+4a2+1)=(2s−(4a−2))(x−s) y=(2s−4a+2)x−s2+4a2+1→エ,オ,カ,キ,ク　② ①②の係数を比較すると 2t+2=2s−4a+2 −t2+1=−s2+4a2+1 簡単にすると s−t=2 (s−t)(s+t)=4a2 すなわち s−t=2 s+t=2a t=0, s=2a→ケ,コ したがって，ℓの方程式は y=2x+1→サ,シ →解説を隠す←

(2)　二つの放物線C, Dの交点のx座標はスである。 　Cと直線ℓ，および直線x=スで囲まれた図形の面積をSとすると， S= aセ ソ である。 (3)　とする。二つの放物線C, Dと直線ℓで囲まれた図形の中で0≦x≦1を満たす部分の面積Tは,a>タのとき，aの値によらず T= チ ツ であり，タのとき T=−テa3+トa2−ナa+ ニ ヌ である。 (4)　次に，(2)(3)で定めたS, Tに対して，U=2T−3Sとおく。aがタの範囲を動くとき，Uは a= ネ ノ で最大値 ハ ヒフ をとる。

解説を読む 二つの放物線C, Dの交点のx座標は，次の連立方程式から y=x2+2x+1･･･(C) y=x2−(4a−2)x+4a2+1･･･(D) C−D辺々引く 4ax−4a2=0（仮定により，a>0） 4a(x−a)=0 x=a→ス →セ,ソ a>1のとき→タ →チ,ツ のとき Dとℓのy座標の差は x2−(4a−2)x+4a2+1−(2x+1)=(x−2a)2 →テ,ト,ナ,ニ,ヌ 数学Ⅱまでの範囲で を ア）　公式として覚えてもよい． イ）　覚えていなくても，この問題のようにn=2のレベルなら，展開してから積分しても，十分間に合う． ウ）　また，数学Ⅲまで習えば，簡単な置換積分によりこの公式を作ることができる． a 1 × + 0 − × U × M × のとき最大値 をとる→ネ,ノ,ハ,ヒフ →解説を隠す←